每本高思课本开头,都有一个叫“知识树”的模块,这东西真是个宝藏。
“树”一共有7棵,对应小学奥数七大模块,树上的每一片“叶子”对应一个知识点,也就是书中的一个章节,黄色的叶子代表本书中涉及到的章节(本文以四年级下册举例)。
树的侧面用数字标注了建议学习的年级,从1到6依次是1年级到6年级,叶子的高度就对应了相应的年级。
有的树上方还有2到3个气球,代表某个专题的综合性章节。
需要注意的是,根据实际学习体会,现在卷的程度越来越激烈,导致这个年级分级已经落后于实际情况。比如在书中标注为5年级的学习内容,在机构的班课中可能4年级甚至3年级就学了,而且机构的课程进度设计是5年级甚至4年级就学完全部七大模块,剩下的1-2年专用于复习、刷题和拿奖。
所以这个进度只作为参考,还是以内容为主。下面就把各个模块都摸排一遍,按照内容的多寡(叶子的数量)排序。
全部看一遍之后,心中有数了,最后我再根据自家普娃目前的学习情况,按照学习重要性对各个模块进行排序,制订具体学习计划。
模块一:应用题(约80个章节)—— 最重要的基本盘,必须拿下
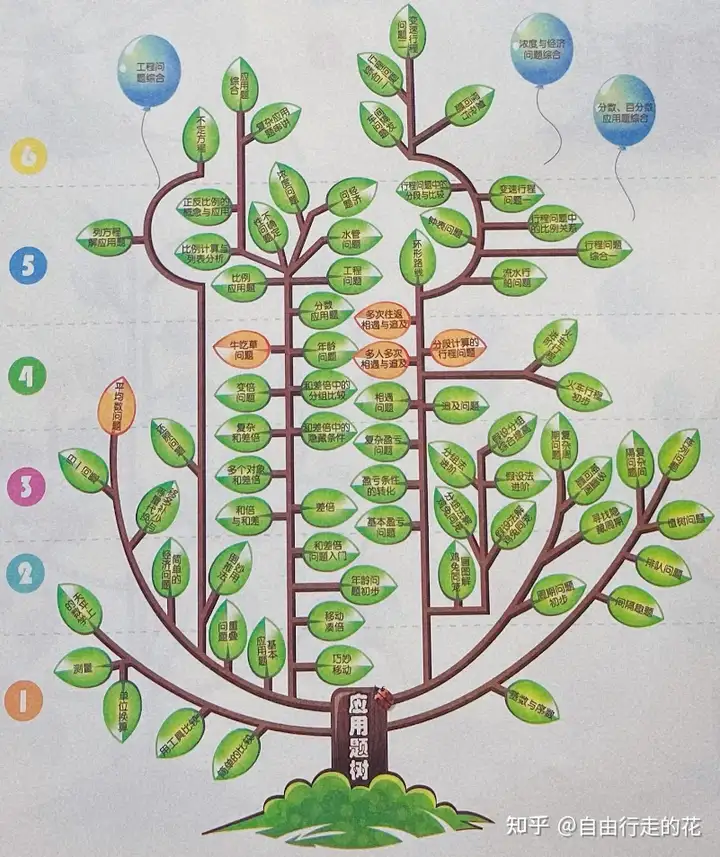
毫无疑问,应用题是小学奥数里面最大的模块,里面主要涉及的应用题类型包括:
一二年级:间隔问题、排队问题、周期问题(初步)、鸡兔同笼(图解法)、年龄问题(初步)、和差倍问题(入门)、倒推法、重叠问题、简单经济问题
三四年级:植树问题、阵列问题、复杂间隔问题、复杂周期问题、鸡兔同笼(假设法和分组法)、基本和复杂盈亏问题、复杂和差倍、年龄问题、还原问题、归一问题、等量代换、行程问题(初步)、追及和相遇问题、牛吃草问题、平均数问题(可以看到绝大部分的应用题类型在三年级就讲完了)
五六年级:复杂行程问题(流水行船、变速行程、环形路线、钟表问题、比例关系)、经济问题、水管问题、工程问题、浓度问题、不确定性问题、比例问题(正反比例)、列方程解应用题、不定方程
模块二:计算(37个章节)—— 也是基本盘,计算是一切的基础,除了小升初,还能为中学助力,必须拿下
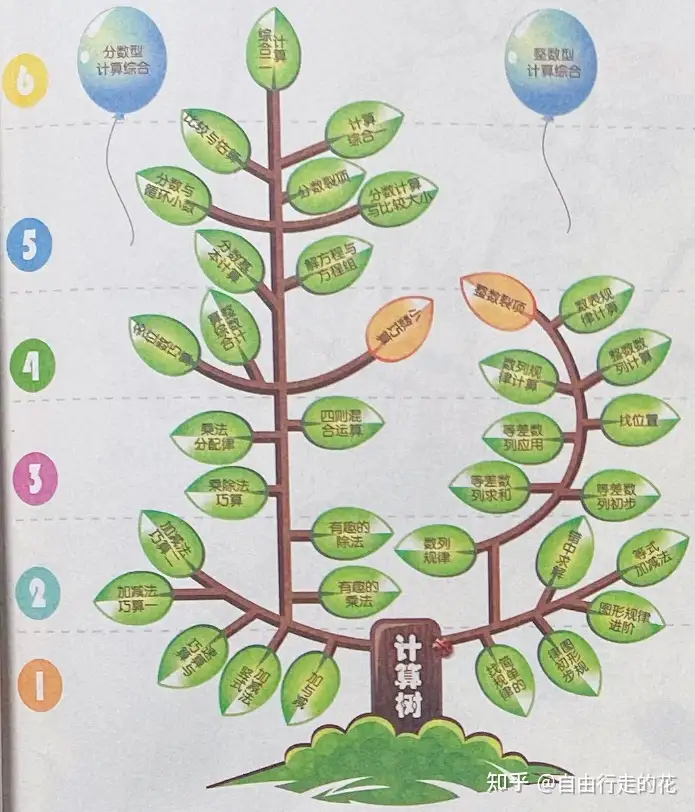
一二年级:速算与巧算、加减法竖式、找简单规律(数字和图形规律)、数列规律、乘除法基础
三四年级:等差数列、乘法分配律、乘除法巧算、四则混合运算、数列规律计算、数表规律计算、整数裂项、小数巧算、多位数巧算、整数计算综合(整数和小数)
五六年级:分数计算与比较大小、分数与循环小数、分数裂项、比较与估算、解方程与方程组(分数)
模块三:组合数学(37个章节)—— 所有模块中次难,拔高,对普娃来说优先级靠后
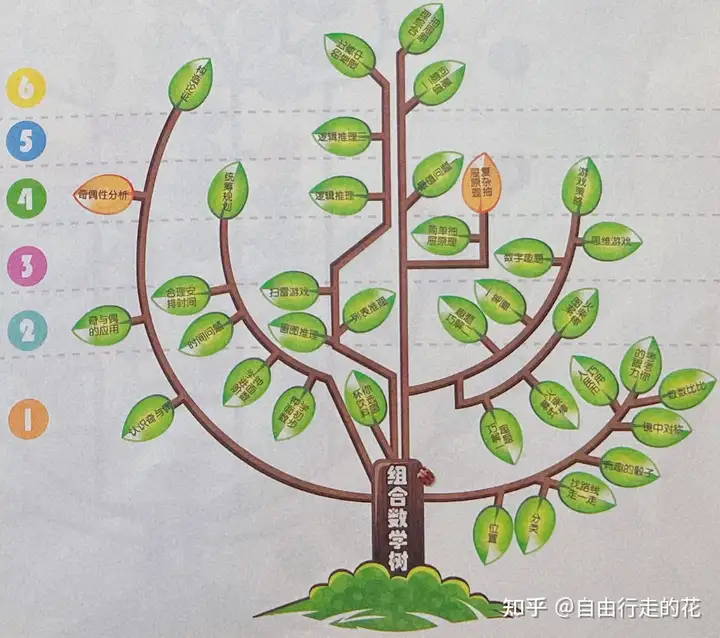
一二年级:位置、分类、找路线、对称、时间问题、奇数和偶数、推理(画图和列表)、一笔画等
三四年级:游戏策略、抽屉原理、最值问题、逻辑推理(如体育比赛问题)、统筹规划、奇偶性分析
五六年级:复杂逻辑推理、比赛中的推理、复杂最值问题、抽屉原理综合、构造论证
模块四:几何(31个章节)—— 中间盘,难度不是很高,尽量拿下

一二年级:拼图、角的初步、立体图形初步、立体图形展开、图形变换
三四年级:几何图形剪拼、长度计算、角度计算、基本直线形面积计算、等积变形、格点图形面积计算、割补法
五六年级:直线形计算中的倍数和比例关系、复杂直线形计算、(等高模型、鸟头模型、风筝模型、)燕尾模型、沙漏与金字塔模型、圆与扇形、直线形计算综合、曲线形计算综合、几何综合(重头戏从五年级开始)
模块五:计数(29个章节)—— 所有模块中次难(与组合数学接近),拔高,对普娃来说优先级靠后
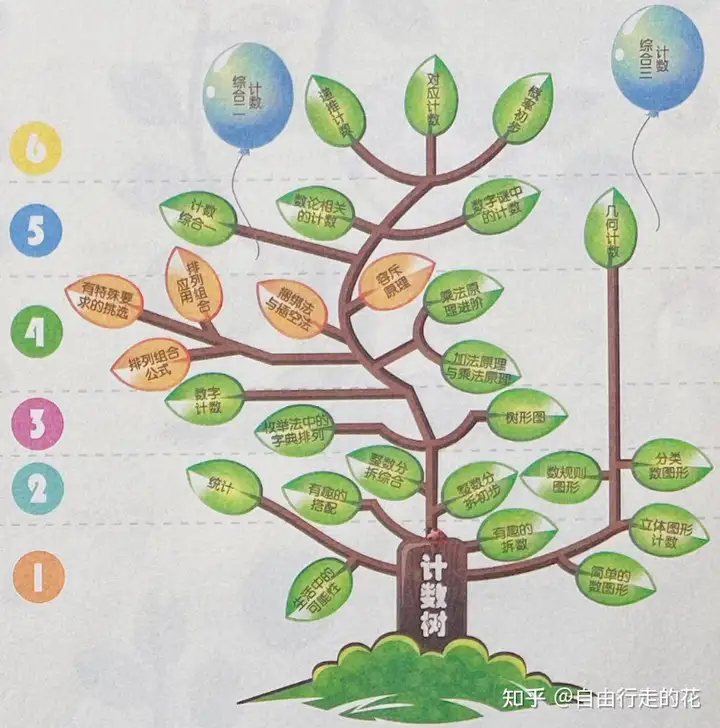
一二年级:可能性初步、图形计数、整数分拆、统计初步
三四年级:树形图、枚举法(字典排列)、数字计数、加乘原理、容斥原理、捆绑法与插空法、排列组合公式与应用、有特殊要求的挑选(加乘原理是重头戏,是后面各种计数问题的基础)
五六年级:数字谜计数、数论相关计数、概率初步、对应计数、递推计数、计数综合
模块六:数字谜(20个章节)—— 扫尾盘,优先级靠后
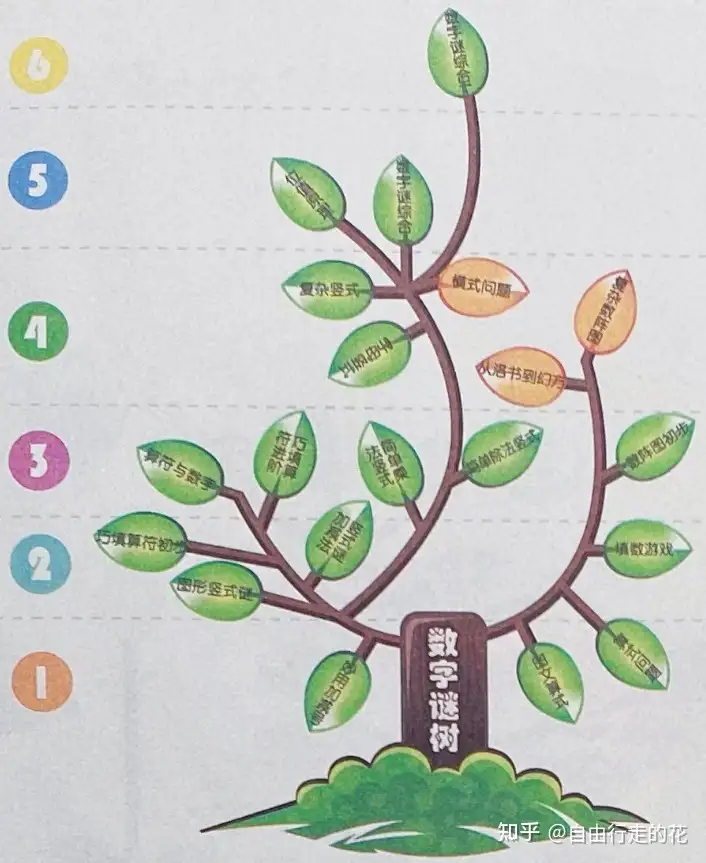
一二年级:算式问题、填数游戏、竖式谜、巧填算符初步
三四年级:数阵图、简单乘除法竖式、巧填算符进阶、算符与数字、幻方、字母竖式、复杂竖式、横式问题
五六年级:位值原理、数字谜综合
模块七:数论(13个章节)—— 所有模块中最难,拔高,对普娃来说优先级靠后
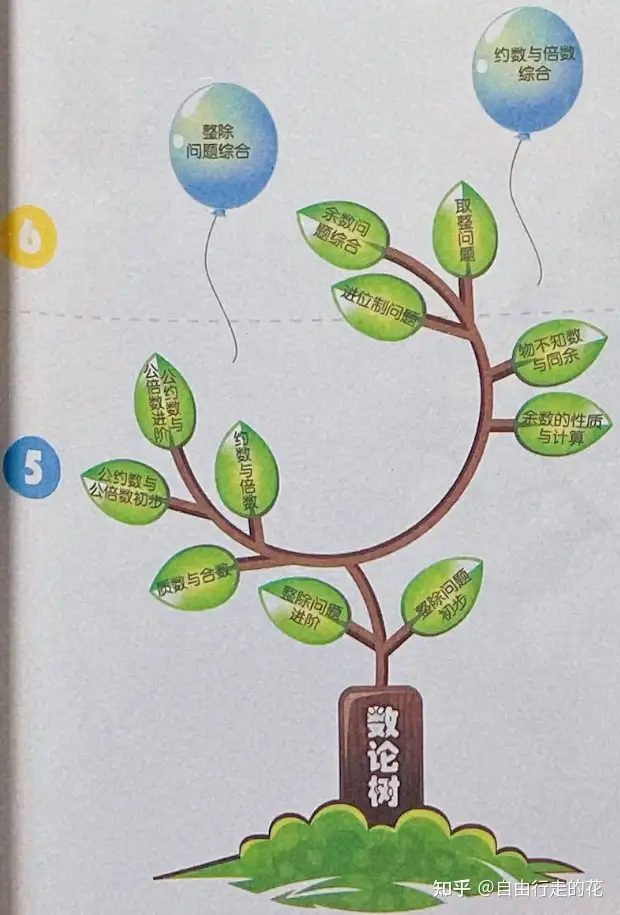
一二年级:无
三四年级:无
五六年级:整除问题、质数与合数、约数与倍数、公约数与公倍数、余数的性质与计算、取整问题、进位制问题
给我家孩子制订的短期学习计划
对我家普娃来说,我认为各模块的学习重要性可以做如下排序:
计算 > 应用题 > 几何 > 计数 > 其他
这几部分都多多少少学过了,孩子基本能听懂,复习巩固一下性价比比较高。
至于听不懂、无法理解的,直接放弃,先保住基本盘。
之所以把后面的模块全部归为“其他”,是因为时间有限,一共只有一周左右完整时间,和后面各种零零碎碎抠出来的时间,中间还要穿插希望杯的备考刷题,具体点说就是争取把2022希望杯100题和近3年真题过一遍。
这些任务叠加在一起,能完成4个模块的全面复习,已经很不容易了。
如果学习效果喜出望外(小概率),省出来一些时间,计划学习余数的性质和计算。
余数我们之前没有专门学习过,估计这一大坨就够我们喝一壶、喝到过年了……